物理信息神经网络(Physics-Informed Neural Networks):一种用于求解非线性偏微分方程正问题和反问题的深度学习框架。
摘要
物理感知神经网络- -在尊重由一般非线性偏微分方程描述的任何给定物理定律的情况下,训练用于解决监督学习任务的神经网络。
在本工作中,我们将在解决两类主要问题的背景下介绍我们的进展:数据驱动的偏微分方程求解和数据驱动的偏微分方程发现。
根据可用数据的性质和排列方式,我们设计了两种不同类型的算法,即连续时间和离散时间模型。
第一类模型形成了一类新的数据有效的时空函数逼近器(data-efficient spatio-temporal function approximators),而第二类模型允许使用任意精度的隐式Runge - Kutta时间步进(stepping)格式,其级数(stages)不受限制。
通过流体、量子力学、反应扩散系统和非线性浅水波传播中的一系列经典问题证明了所提框架的有效性。
1. 介绍
随着可用数据和计算资源的爆炸式增长,机器学习和数据分析的最新进展在不同的科学学科中产生了变革性的结果,包括图像识别,认知科学和基因组学。然而,在分析复杂物理、生物或工程系统的过程中,数据获取的成本往往是高昂的,我们不可避免地面临着在部分信息下得出结论和做出决策的挑战。在这种小数据环境下,绝大多数先进的机器学习技术(例如,深度/卷积/循环神经网络)缺乏鲁棒性,无法提供任何收敛性保证。
最初,训练深度学习算法的任务从少数-潜在的非常高维的输入和输出数据对中准确地识别非线性映射似乎是最幼稚的。值得注意的是,在许多物理和生物系统建模的案例中,存在着大量的先验知识,而这些知识目前还没有被用于现代机器学习实践中。设是原则性的物理规律控制着系统的时变动力学,或者是一些经验性验证的规则或其他领域的专门知识,这些先验信息可以作为正则化代理,将可容许解的空间限制在可管理的大小(例如,在不可压缩流体动力学问题中,通过丢弃任何违反质量守恒原则的非现实流动解)。反过来,将这些结构化信息编码到一个学习算法中,可以放大算法所看到的数据的信息内容,使其能够快速地转向正确的解决方案,即使只有很少的训练实例也能很好地泛化。
在这里,作者使用高斯过程回归来设计针对给定线性算子的函数表示,并且能够准确地推断解决方案,并为数学物理中的几个原型问题提供不确定性估计。
Raissi等人在随后的研究中在推理和系统辨识(inference and systems identification)两种情况下提出了对非线性问题的扩展[ 8、9 ]。尽管高斯过程在编码先验信息方面具有灵活性和数学优雅性,但对非线性问题的处理引入了两个重要的限制。首先,在[ 8、9 ]中,作者必须在时间上对任何非线性项进行局部线性化,从而限制了所提出的方法在离散时间域的适用性,并损害了其在强非线性区域中预测的准确性。其次,高斯过程回归的贝叶斯性质需要一定的先验假设,这可能会限制模型的表达能力,并导致稳健性/脆性问题,特别是对于非线性问题[ 10 ]。
2. 问题设置
在本工作中,我们采取了一种不同的方法,使用深度神经网络,并利用它们作为通用函数逼近器的已知能力[ 11 ]。在这种情况下,我们可以直接处理非线性问题,而不需要任何先验假设、线性化或局部时步。我们利用自动微分(automatic differentiation)的最新进展 - -科学计算中最有用但可能未被充分利用的技术之一- -对神经网络的输入坐标和模型参数进行微分,以获得物理信息的神经网络。这类神经网络被限制在遵守任何对称性、不变性或守恒原则,这些原则源于控制观测数据的物理规律,如一般的时间依赖和非线性偏微分方程所建模。这种简单而强大的结构使我们能够处理计算科学中广泛的问题,并引入了一种潜在的变革性技术,导致了新的数据效率和物理信息的学习机的发展,新的偏微分方程数值求解器的类别,以及新的数据驱动的方法用于模型反演和系统识别。
这项工作的总体目标是为在数学物理的长期发展中丰富深度学习的建模和计算新范式奠定基础。为此,我们的手稿分为两个部分,旨在介绍我们在两类主要问题背景下的发展:数据驱动的解决方案和数据驱动的偏微分方程发现(data-driven solution and data-driven discovery of partial differential equations)。代码链接。在整个工作中,我们一直使用相对简单的具有双曲正切激活函数的深度前馈神经网络结构,并且没有额外的正则化(例如, L1 / L2 penalties、dropout等)。本文中的每个数值例子都伴随着对我们所使用的神经网络结构的详细讨论,以及它的训练过程(例如优化器optimizer、学习率learning rates等)的细节。最后,在附录A和附录B中提供了一系列旨在证明所提出方法性能的系统研究。
在这项工作中,我们考虑一般形式的参数化和非线性偏微分方程: \[ u_t+\mathcal{N}[u;\lambda]=0, x\in\Omega, t\in[0,T] \tag{1} \] 其中\(u(t,x)\)表示隐(潜)解--latent(hidden) solution,\(\mathcal{N}[\cdot;\lambda]\)是以λ为参数的非线性算子(nonlinear operator parametrized by λ),Ω是\(\mathbb{R}^{D}\)的子集。该设置涵盖了包括守恒定律、扩散过程、对流-扩散-反应方程系统和动力学方程在内的广泛的数学物理问题。作为一个激励例子,一维Burgers方程[ 13 ]对应于\(\mathcal{N}[u;\lambda]=\lambda_1uu_x-\lambda_2u_{xx}\),\(\lambda=(\lambda_1,\lambda_2)\)的情况。在这里,下标表示在时间或空间上的部分微分。给定系统的噪声测量,我们感兴趣的是解决两个不同的问题。第一个问题是关于偏微分方程[ 4、8]的推断(inference),滤波(filtering)和平滑(smoothing),或数据驱动的解(data-driven)的问题,它指出:given fixed model parameters λ what can be said about the unknown hidden state u(t, x) of the system? 第二个问题是学习(learning)、系统辨识(system identification)或数据驱动的偏微分方程发现(data-driven discovery of partial differential equations)问题[ 5、9、14],即:what are the parameters λ that best describe the observed data
3. 偏微分方程的数据驱动解法
让我们首先集中于计算一般形式的偏微分方程(即上述第一个问题)的数据驱动解的问题: \[ u_t+\mathcal{N}[u]=0, x\in\Omega, t\in[0,T] \tag{2} \] 其中\(u(t,x)\)表示隐(潜)解--latent(hidden) solution,\(\mathcal{N}[\cdot]\)是一个非线性微分算子(nonlinear differential operator),Ω是\(\mathbb{R}^{D}\)的子集。在3.1节和3.2节中,我们提出了两种不同类型的算法,即连续时间模型和离散时间模型,并通过不同的基准问题突出了它们的性质和性能。在我们研究的第二部分(见第4节)中,我们将注意力转移到数据驱动的偏微分方程发现问题[ 5、9、14]上。
3.1. 连续时间模型
我们定义\(f(t,x)\)由方程( 2 )的左端给出;即: \[ f:=u_t+\mathcal{N}[u] \tag{3} \] 并通过深度神经网络逼近\(u(t,x)\)。这个假设和方程( 3 )一起产生了一个物理信息的神经网络\(f(t,x)\)。该网络可以通过应用链式规则来导出,用于使用自动微分来区分函数的组成[ 12 ],并且具有与代表u( t , x)的网络相同的参数,尽管由于微分算子\(\mathcal{N}\)的作用而具有不同的激活函数。神经网络\(u(t,x)\)和\(f(t,x)\)之间的共享参数可以通过最小化均方误差损失(mean squared error loss)来学习: \[ MSE=MSE_u+MSE_f \tag{4} \] 其中 \[ MSE_u=\frac1{N_u}\sum_{i=1}^{N_u}|u(t_u^i,x_u^i)-u^i|^2, \]
\[ MSE_f=\frac1{N_f}\sum_{i=1}^{N_f}|f(t_f^i,x_f^i)|^2. \]
其中,\(\{t_u^i,x_u^i,u^i\}_{i=1}^{N_u}\)表示\(u(t,x)\)上的初始和边界训练数据,\(\{t_f^i,x_f^i\}_{i=1}^{N_f}\)为\(f(t,x)\)指定的搭配点(specify the collocation points)。损失\(MSE_u\)对应于初始和边界数据,而\(MSE_f\)在有限的配置点(collocation points)集合上强制方程( 2 )施加的结构。虽然类似的利用物理规律约束神经网络的想法在之前的研究中已经被探索过[ 15、16 ],但在这里我们利用现代计算工具重新审视它们,并将它们应用于由时间依赖的非线性偏微分方程描述的更具挑战性的动力学问题。
在这里,我们应该强调这条工作路线与现有文献中阐述机器学习在计算物理中使用的方法之间的重要区别。物理信息机器学习(physics-informed machine learning)这个术语最近也被Wang等人在湍流建模方面使用[ 17 ]。所有这些方法都使用机器学习算法,如支持向量机(support vector machines)、随机森林(random forests)、高斯过程(Gaussian processes)和前馈/卷积/循环神经网络(feed-forward/convolutional/recurrent neural networks)仅仅作为黑盒工具。如上所述,拟议的工作旨在更进一步,重新考虑根据底层差分运算符定制的"自定义"激活和损失函数的构造。这使得我们可以通过理解和欣赏深度学习领域内自动差异化所发挥的关键作用来打开黑箱。一般的自动微分,特别是反向传播算法,是目前训练深度模型的主要方法,通过取其关于模型参数(例如,权重和偏差)的导数。在这里,我们使用深度学习社区使用的完全相同的自动微分技术,通过对其输入坐标(即,空间和时间)的导数来为神经网络提供物理信息,其中物理由偏微分方程描述。我们从经验上观察到,这种结构化方法引入了一种正则化机制,允许我们使用相对简单的前馈神经网络架构,并使用少量数据对其进行训练。这种简单想法的有效性可能与Lin,Tegmark和罗尔尼克[ 30 ]的言论有关,并提出了许多有趣的问题,需要在未来的研究中定量处理。
在所有数据驱动偏微分方程求解的情况下,训练数据\(N_u\)的总数相对较少(几百到几千分),我们选择使用L - BFGS,一种基于准牛顿(quasi-Newton)、全批次梯度(full-batch gradient-based)的优化算法来优化所有损失函数[ 35 ]。对于更大的数据集,例如第4节中讨论的数据驱动模型发现实例,可以很容易地使用随机梯度下降(stochastic gradient descent )及其现代变体[ 36、37 ]来使用计算效率更高的小批量设置。尽管没有理论上保证该过程收敛到全局最小值,但我们的经验证据表明,如果给定的偏微分方程是适定的且其解是唯一的,那么在具有足够表达能力的神经网络结构和足够数量的配置点(collocation points)\(N_f\)的情况下,我们的方法能够达到很好的预测精度。这一般性观察与方程4的均方误差损失所导致的优化空间(optimization landscape)有着深刻的联系,并定义了一个与深度学习[ 38、39 ]近期理论发展同步的开放性研究问题。为此,我们将使用附录A和附录B中提供的一系列系统的敏感性研究来检验所提出方法的稳健性。
3.1.1. Example(Shrodinger Equation)
这个例子旨在突出我们的方法处理周期边界条件、复值解以及控制偏微分方程中不同类型非线性项的能力。一维非线性薛定谔方程是研究量子力学系统的经典场方程,包括光纤和/或波导中的非线性波传播、玻色-爱因斯坦凝聚体、等离子体波等。在光学中,非线性项来自于给定材料的强度依赖折射率。类似地,玻色-爱因斯坦凝聚体的非线性项是相互作用的N体系统的平均场相互作用的结果。带有周期边界条件的非线性薛定谔方程为: \[ \begin{aligned} &ih_{t}+0.5h_{xx}+|h|^{2}h=0,\quad x\in[-5,5],\quad t\in[0,\pi/2], \\ &h(0,x)=2 \mathrm{sech}(x), \\ &h(t,-5)=h(t,5), \\ &h_x(t,-5)=h_x(t,5), \end{aligned} \tag{5} \] 其中\(h(t,x)\)为复值解(complex-valued solution)。定义\(f(t,x)\)为: \[ f:=ih_t+0.5h_{xx}+|h|^2h, \] 并在\(h(t,x)\)上放置一个复值神经网络先验。事实上,如果\(u\)表示\(h\)的实部,\(v\)为虚部,我们将多输出神经网络先验置于\(h(t,x) = \begin{bmatrix}u(t,x)&v(t,x)\end{bmatrix}\)这将产生复值(多输出)物理信息神经网络\(f(t,x)\)。神经网络\(h(t,x)\)和\(f(t,x)\)的共享参数可以通过最小化均方误差损失来学习: \[ MSE=MSE_0+MSE_b+MSE_f \tag{6} \] 其中 \[ MSE_0=\frac1{N_0}\sum_{i=1}^{N_0}|h(0,x_0^i)-h_0^i|^2, \]
\[ MSE_b=\frac1{N_b}\sum_{i=1}^{N_b}\left(|h^i(t_b^i,-5)-h^i(t_b^i,5)|^2+|h_x^i(t_b^i,-5)-h_x^i(t_b^i,5)|^2\right), \]
\[ MSE_f=\frac{1}{N_f}\sum_{i=1}^{N_f}|f(t_f^i,x_f^i)|^2. \]
其中,\(\{x_0^i,h_0^i\}_{i=1}^{N_0}\)表示初始数据,\(\{t_b^i\}_{i=1}^{N_b}\)对应边界上的配置点,\(\{t_f^i,x_f^i\}_{i=1}^{N_f}\)表示\(f(t,x)\)上的配置点。因此,\(MSE_0\)对应于初始数据上的损失,\(MSE_b\)执行周期性边界条件,\(MSE_f\)惩罚配置点上不满足的薛定谔方程。为了评估我们方法的准确性,我们模拟了方程( 5 ),使用传统的光谱方法来创建高分辨率的数据集。具体来说,从初始状态\(h(0,x)=2\) \(sech(x)\)出发,假设周期边界条件\(h(t,-5)=h(t,5)\)和\(h_x(t,-5)=h_x(t,5)\),利用Chebfun程序包[ 40 ],采用256模式的谱Fourier离散和四阶显式Runge - Kutta时间积分器,在时间步长为\(\Delta t=π/2·10^{-6}\)的情况下,积分方程( 5 )到最终时间\(t=π/2\)。在我们的数据驱动设定下,我们观察到的都是潜函数\(h(t,x)\)在t=0时刻的测量值\(\{x_0^i,h_0^i\}_{i=1}^{N_0}\)。特别地,训练集由从完整高分辨率数据集中随机解析出的\(h(0,x)\)上共\(N_0=50\)个数据点,以及\(N_b=50\)个随机采样的用于增强周期边界的配置点\(\{t_b^i\}_{i=1}^{N_b}\)组成。此外,我们假设\(N_f = 20000\)个随机取样的配置点,用于在求解域内执行式( 5 )。所有随机采样的点位置使用空间填充拉丁超立方采样策略[ 41 ]生成。
这里我们的目标是推导出薛定谔方程( 5 )的全部时空解h( t , x) 。我们选择使用每层100个神经元的5层深度神经网络和双曲正切激活函数来联合表示隐函数\(h(t,x) = \begin{bmatrix}u(t,x)&v(t,x)\end{bmatrix}\)。一般来说,为了适应\(u( t , x)\)的预期复杂度,神经网络应该被赋予足够的逼近能力。虽然可以使用更系统的程序,如贝叶斯优化[ 42 ]来微调神经网络的设计,但在缺乏理论误差/收敛性估计的情况下,神经结构/训练过程与基础微分方程复杂性之间的相互作用仍然知之甚少。 通过采用贝叶斯方法和监测预测后验分布的方差来评估预测解的准确性是一条可行的途径,但这超出了本工作的范围,将在未来的研究中进行研究。
在这个例子中,我们的设置旨在强调所提出的方法相对于众所周知的过拟合问题的鲁棒性。具体来说,式( 6 )中的\(MSE_f\)项作为正则化机制,惩罚不满足式( 5 )的解。因此,物理信息神经网络的一个关键特性是可以使用小数据集进行有效的训练;在物理系统的研究中经常会遇到这样的设定,数据获取的成本可能是令人望而却步的。Figure 1总结了实验结果。具体来说,图1顶部面板显示了预测时空解(predicted spatio-temporal solution)\(|h(t,x)|=\sqrt{u^2(t,x)+v^2(t,x)}\)的大小,以及初始和边界训练数据的位置。所有得到的预测误差针对该问题的测试数据进行验证,并在相对范数\(\mathbb L_2\)下测量为\(1.97·10^{-3}\)。图1的下面部分给出了对预测解的更详细的评估。特别地,我们给出了不同时刻t = 0.59,0.79,0.98的精确解和预测解的比较。利用少量的初始数据,物理信息神经网络可以准确地捕捉薛定谔方程的复杂非线性行为。迄今为止所考虑的连续时间神经网络模型的一个潜在限制是需要使用大量的配置点Nf,以便在整个时空域中执行物理信息约束。虽然这对一个或两个空间维度的问题没有显著的影响,但可能会在更高维的问题中引入严重的瓶颈,因为全局执行物理信息约束(即,在我们的情况下,一个偏微分方程)所需的配置点总数将呈指数增长。虽然这种限制在一定程度上可以通过使用稀疏网格或拟蒙特卡罗采样方案[ 43、44 ]来解决,但在接下来的章节中,我们提出了一种不同的方法,利用经典的Runge - Kutta时间步进方案,提出了一种更结构化的神经网络表示方法。
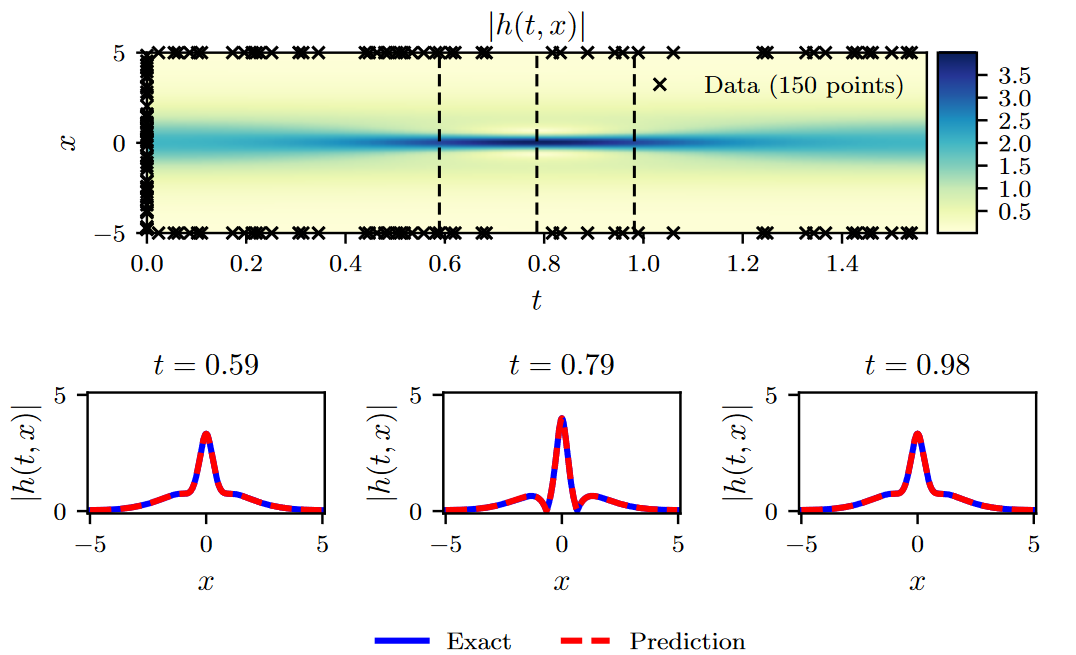
Figure 1. 薛定谔方程:Top:预测解\(| h( t , x) |\)以及初始和边界训练数据。此外,我们使用了20,000个使用拉丁超立方体采样策略生成的搭配点。Bottom:顶部面板中虚线竖线所描绘的三个时间快照对应的预测解和精确解的比较。The relative \(\mathbb L_2\) error for this casr is \(1.97·10^{-3}\).
3.2. 离散时间模型
我们将q stages的Runge - Kutta方法的一般形式[ 45 ]应用于方程( 2 ),得到: \[ \begin{aligned}&u^{n+c_i}=u^n-\Delta t\sum_{j=1}^qa_{ij}\mathcal{N}[u^{n+c_j}],&i=1,\ldots,q,\\&u^{n+1}=u^n-\Delta t\sum_{j=1}^qb_j\mathcal{N}[u^{n+c_j}].\end{aligned} \tag{7} \] 这里\(u^{n+c_j}(x) = u(t^n+c_j\Delta t,x) \mathrm, j = 1,\ldots,q.\)这种通用形式同时包含隐式和显式时间步进格式,取决于参数\(\{ a_{ij},b_j,c_j\}\)的选择。式(7)可以等价表示为: \[ \begin{aligned}&u^n=u_i^n,\quad i=1,\ldots,q,\\&u^n=u_{q+1}^n,\end{aligned} \tag{8} \] 其中 \[ \begin{aligned}&u_{i}^{n}:=u^{n+c_i}+\Delta t\sum_{j=1}^qa_{ij}\mathcal{N}[u^{n+c_j}],\quad i=1,\ldots,q,\\&u_{q+1}^{n}:=u^{n+1}+\Delta t\sum_{j=1}^qb_j\mathcal{N}[u^{n+c_j}].\end{aligned} \tag{9} \] 我们通过放置一个多输出神经网络先验来进行: \[ \begin{bmatrix}u^{n+c_1}(x),\ldots,u^{n+c_q}(x),u^{n+1}(x)\end{bmatrix}. \tag{10} \] 这一先验假设与式( 9 )一起构成了一个以\(x\)为输入和输出的物理信息神经网络: \[ \begin{bmatrix}u_1^n(x),\ldots,u_q^n(x),u_{q+1}^n(x)\end{bmatrix}. \tag{11} \]
3.2.1. Example (Allen-Cahn Equation)
这个例子旨在突出所提出的离散时间模型处理控制偏微分方程中不同类型非线性的能力。为此,我们考虑带有周期边界条件的Allen - Cahn方程: \[ \begin{aligned} &\begin{aligned}u_t-0.0001u_{xx}+5u^3-5u=0,\quad x\in[-1,1],\quad t\in[0,1],\end{aligned} \\ &\begin{aligned}u(0,x)=x^2\cos(\pi x),\end{aligned} \\ &u(t,-1)=u(t,1), \\ &u_x(t,-1)=u_x(t,1). \end{aligned} \tag{12} \] Allen - Cahn方程是反应扩散系统(reaction-diffusion)中的一个著名方程。它描述了多元合金体系(multicomponent alloy systems)中的相分离过程,包括有序-无序转变。对于Allen - Cahn方程,方程( 9 )中的非线性算子由下式给出: \[ \mathcal{N}[u^{n+c_j}]=-0.0001u_{xx}^{n+c_j}+5\left(u^{n+c_j}\right)^3-5u^{n+c_j}, \] 神经网络( 10 )和( 11 )的共享参数可以通过最小化误差平方和来学习: \[ SSE=SSE_n+SSE_b, \tag{13} \] 其中 \[ SSE_n=\sum_{j=1}^{q+1}\sum_{i=1}^{N_n}|u_j^n(x^{n,i})-u^{n,i}|^2, \]
\[ \begin{aligned}SSE_b&=\quad\sum_{i=1}^q|u^{n+c_i}(-1)-u^{n+c_i}(1)|^2+|u^{n+1}(-1)-u^{n+1}(1)|^2\\&+\quad\sum_{i=1}^q|u_x^{n+c_i}(-1)-u_x^{n+c_i}(1)|^2+|u_x^{n+1}(-1)-u_x^{n+1}(1)|^2.\end{aligned} \]
其中,\(\{x^{n,i},u^{n,i}\}_{i=1}^{N_n}\)对应于\(t^n\)时刻的数据。在经典的数值分析中,由于显式格式的稳定性约束或隐式格式的计算复杂度约束,这些时间步长通常被限制在很小的范围内[ 45 ]。这些约束随着Runge - Kutta级数q的增加而变得更加严重,对于大多数实际问题,需要花费数千到数百万个这样的步骤,直到求解到期望的最终时间。与经典方法形成鲜明对比的是,这里可以使用任意多步的隐式Runge - Kutta格式,有效地减少额外的成本(准确地说,只是神经网络最后一层的参数个数随阶段总数线性增加。)。这使得我们可以采取非常大的时间步长,同时保持稳定性和较高的预测精度,从而使我们能够在一个步骤中解决整个时空解。
在这个例子中,我们通过使用传统的谱方法模拟Allen - Cahn方程( 12 )生成了一个训练和测试数据集。具体来说,从初始条件\(u(0,x)=x^2cos(πx)\)出发,假设周期边界条件\(u(t,-1)=u(t,1)\)和\(u_x(t,-1)=u_x(t,1)\),we have integrated equation (12) up to a final time t = 1.0 using the Chebfun package [40] with a spectral Fourier discretization with 512 modes and a fourth-order explicit Runge-Kutta temporal integrator with time-step \(∆t = 10^{−5}\).
我们的训练数据集由\(N_n = 200\)个初始数据点组成,这些初始数据点是从t = 0.1时刻的精确解中随机子采样得到的,目标就是在t = 0.9时刻用一个大小为∆t = 0.8的单时间步(single time-step)预测解。为此,我们采用具有4个隐含层和每层200个神经元的离散时间物理信息神经网络,而输出层预测101个感兴趣的量,对应于q = 100的Runge - Kutta级数\(u^{n + c_i} ( x ),i = 1,..,q\)和最终时间\(u^{n + 1} ( x )\)的解。该方案的理论误差估计预示着\(\mathcal O(∆t^{2q} )\)的时间误差累积[ 45 ],在我们的例子中转化为低于机器精度的误差途径,即\(∆t^{2q}=0.8^{200}≈10^{-20}\)。据我们所知,这是首次使用该高阶隐式Runge - Kutta格式。值得注意的是,从t = 0.1处的光滑初始数据出发,我们可以在单个时间步内预测t = 0.9处的近似不连续解,其相对\(\mathbb L_2\)误差为\(6.99·10^{-3}\),如图2所示。这种误差完全归因于神经网络对\(u( t , x)\)的逼近能力,以及误差平方和损失允许对训练数据进行插值的程度。
控制离散时间算法性能的关键参数是Runge - Kutta级数q的总数和时间步长∆t。正如我们在附录A和附录B提供的系统研究中所证明的那样,低阶方法,例如对应于经典梯形法则的q = 1情形,以及对应于四阶Gauss - Legendre方法的q = 2情形,在大时间步长下无法保持其预测精度,因此需要采用小尺寸的多时间步长的求解策略。Moreover, numerical stability is not sacrificed either as implicit Gauss-Legendre is the only family of time-stepping schemes that remain A-stable regardless of their order, thus making them ideal for stiff problems [45].这些性质对于实现这种简单性的算法来说是前所未有的,并说明了我们的离散时间方法的关键亮点之一。
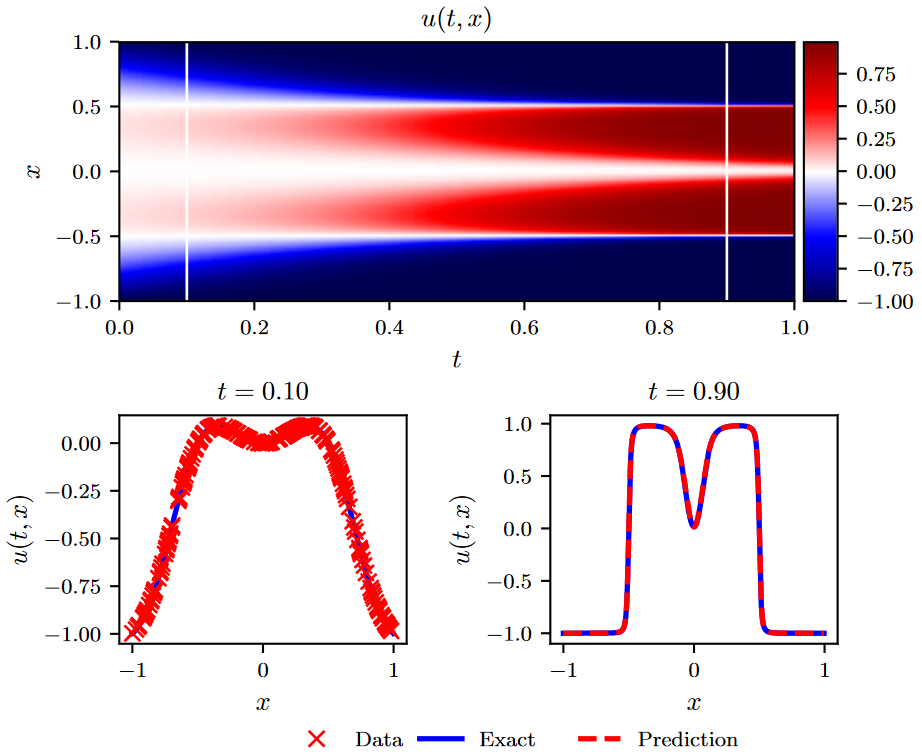
Figure 2. Allen-Cahn equation: Top: Solution u(t, x) along with the location of the initial training snapshot at t = 0.1 and the final prediction snapshot at t = 0.9. Bottom: Initial training data and final prediction at the snapshots depicted by the white vertical lines in the top panel. The relative \(\mathbb L_2\) error for this case is \(6.99·10^{−3}\).
4. 数据驱动的偏微分方程发现
在当前的研究中,我们将注意力转移到数据驱动的偏微分方程的发现问题上[ 5、9、14]。在4.1节和4.2节中,我们提出了两种不同类型的算法:连续时间模型和离散时间模型,并通过各种典范问题的镜头来突出它们的性质和表现。
4.1. 连续时间模型
让我们回忆一下式( 1 ),类似于3.1节,定义\(f(t,x)\)由式( 1 )的左边给出;即: \[ f:=u_t+\mathcal{N}[u;\lambda]. \tag{14} \] 我们通过一个深度神经网络来逼近\(u(t,x)\)。这个假设和式(14)一起产生了一个物理信息神经网络\(f(t,x)\)。这个网络可以通过应用链规则来导出,用于使用自动微分来区分函数的组成[ 12 ]。值得强调的是,微分算子λ的参数变成了物理信息神经网络\(f(t,x)\)的参数。
我们的下一个例子涉及一个由无处不在的Navier - Stokes方程描述的不可压缩流体流动的现实场景。Navier - Stokes方程描述了许多科学和工程感兴趣的物理现象。它们可以用来模拟天气、洋流、管道中的水流和机翼周围的空气流动。Navier - Stokes方程的完整和简化形式有助于飞行器和汽车的设计,血液流动的研究,电站的设计,污染物扩散的分析和许多其他应用。考虑由下式给出的二维Navier - Stokes方程(将所提出的框架直接推广到三维的Navier - Stokes方程): \[ u_t+\lambda_1(uu_x+vu_y)=-p_x+\lambda_2(u_{xx}+u_{yy}),\\v_t+\lambda_1(uv_x+vv_y)=-p_y+\lambda_2(v_{xx}+v_{yy}), \tag{15} \] 其中\(u(t,x,y)\)表示速度场的\(x\)分量,\(v(t,x,y)\)表示\(y\)分量,\(p(t,x,y)\)表示压力,\(\lambda=(\lambda_1,\lambda_2)\)为未知参数。在无散度函数(divergence-free functions)集合中寻找Navier - Stokes方程的解;即, \[ u_x+v_y=0 \tag{16} \] 这个额外的方程是描述流体质量守恒的不可压缩流体的连续性方程。我们作出假设: \[ u=\psi_y,\quad v=-\psi_x, \tag{17} \] 对于某个隐函数\(\psi(t,x,y)\)(利用向量位势的概念,这个构造可以推广到三维问题。)。在此假设下,连续性方程( 16 )将自动满足。给定速度场的噪声测量(noisy measurements) \(\{t^i,x^i,y^i,u^i,v^i\}_{i=1}^{N}\),我们感兴趣的是学习参数λ和压力p( t , x , y)。定义\(f(t,x,y)\)和\(g(t,x,y)\)为: \[ f:=u_t+\lambda_1(uu_x+vu_y)+p_x-\lambda_2(u_{xx}+u_{yy}),\\g:=v_t+\lambda_1(uv_x+vv_y)+p_y-\lambda_2(v_{xx}+v_{yy}), \tag{18} \] 并通过使用具有两个输出的单个神经网络对\(\begin{bmatrix}\psi(t,x,y)&p(t,x,y)\end{bmatrix}\)进行联合逼近。该先验假设与式( 17 )和式( 18 )一起构成物理信息神经网络\(\begin{bmatrix}f(t,x,y)&g(t,x,y)\end{bmatrix}\)。Navier - Stokes算子的参数λ以及神经网络\(\begin{bmatrix}\psi(t,x,y)&p(t,x,y)\end{bmatrix}\)的参数可以通过最小化均方误差损失来训练: \[ \begin{aligned}MSE&:=\quad\frac1N\sum_{i=1}^N\left(|u(t^i,x^i,y^i)-u^i|^2+|v(t^i,x^i,y^i)-v^i|^2\right)\\&+\quad\frac1N\sum_{i=1}^N\left(|f(t^i,x^i,y^i)|^2+|g(t^i,x^i,y^i)|^2\right).\end{aligned} \tag{19} \] 这里我们考虑不可压缩流流过圆柱的原型问题;对于雷诺数\(Re = u_{\infty}D/\nu.\)的不同区域,一个已知的问题表现出丰富的动力学行为和转变。假设无量纲自由流(non-dimensional free stream)速度\(u_{\infty}=1\),圆柱直径(cylinder diameter)\(D = 1\),运动粘度(kinematic viscosity)\(ν = 0.01\),系统表现出周期性的稳态行为,其特征是圆柱尾迹中的非对称涡脱落模式,称为Karman vortex street[ 46 ]。
为了生成这个问题的高分辨率数据集,我们使用了谱/ hp元求解器NekTar [ 47 ]。具体来说,通过由412个三角形单元组成的剖分将求解域在空间上离散化,并在每个单元内将解近似为第十级分层、半正交Jacobi多项式展开的线性组合[ 47 ]。我们假设在左边界施加均匀的自由流速度剖面,在位于圆柱下游25个直径处的右边界施加零压力流出条件,以及[ - 15,25] × [ - 8,8]区域的顶部和底部边界的周期性。我们使用三阶刚性稳定格式[ 47 ]对方程( 15 )进行积分,直到系统达到周期稳态,如图3 ( a )所示。接下来,这个稳态解对应的结果数据集中的一小部分将用于模型训练,而剩余的数据将用于验证我们的预测。为了简单起见,我们选择将采样限制在圆柱下游的一个矩形区域内,如图3 ( a )所示。
考虑到流向\(u( t , x , y)\)和横向\(v( t , x , y)\)速度分量上的数据较为分散且可能存在噪声,我们的目标是识别未知参数\(λ_1\)和\(λ_2\),并获得圆柱尾流中整个压力场\(p( t , x , y)\)的定性精确重建,根据定义只能识别到一个常数。为此,我们通过对完整的高分辨率数据集进行随机子采样,创建了一个训练数据集。为了突出我们的方法从零散且稀缺的训练数据中学习的能力,我们选择了N = 5000,仅相当于可用数据总数的1 %,如图3 ( b )所示。图中还标出了模型训练后预测速度分量\(u( t , x , y)\)和\(v( t , x , y)\)的代表性快照。本文采用的神经网络结构由9层组成,每层包含20个神经元。
本算例的结果汇总如图4所示。我们观察到,即使在训练数据被噪声污染的情况下,基于物理信息的神经网络也能够以非常高的精度正确识别未知参数\(λ_1\)和\(λ_2\)。具体来说,对于无噪声的训练数据,估计\(λ_1\)和\(λ_2\)的误差分别为0.078%和4.67%。当训练数据中含有1%不相关的高斯噪声时,预测结果依然稳健,\(λ_1\)和\(λ_2\)的预测误差分别为0.17%和5.70%。
一个更有意思的结果源于该网络能够在没有关于压力本身的任何训练数据的情况下,对整个压力场\(p( t , x , y)\)提供定性准确的预测。对于一个代表性的压力快照,图4给出了与精确压力解的直观对比。注意到精确压力和预测压力之间的大小差异是由不可压缩Navier - Stokes系统的性质所决定的,因为压力场只有在一个常数范围内是可识别的。这种利用底层物理从辅助测量中推断感兴趣的连续量的结果是物理信息神经网络所具有的增强能力的一个很好的例子,并突出了它们在解决高维反问题方面的潜力。
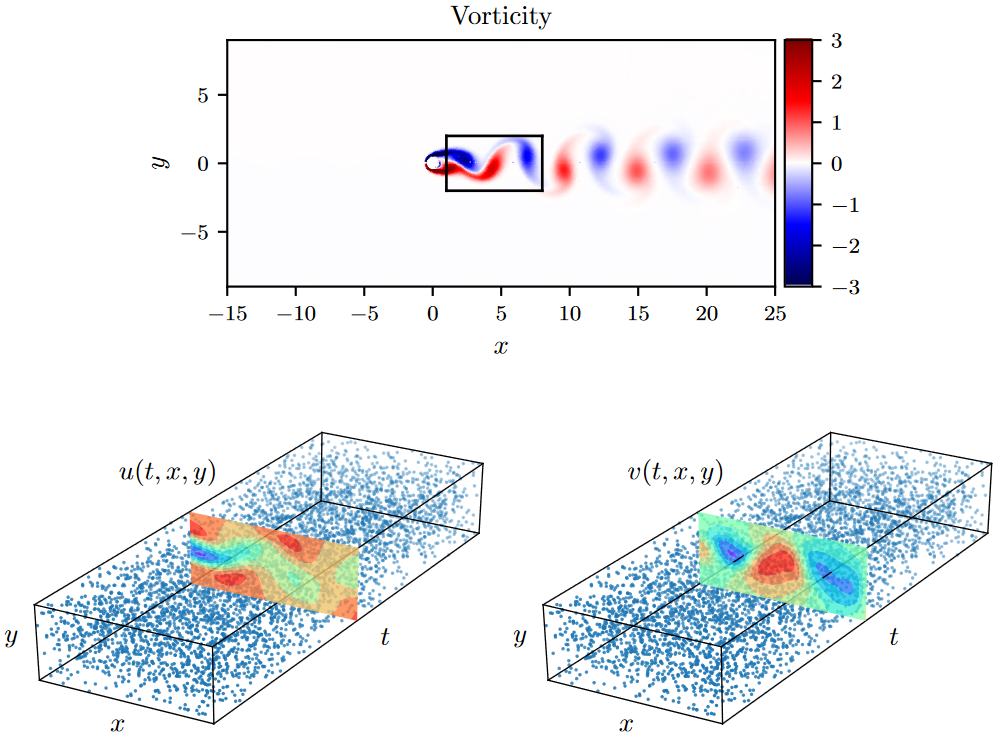
Figure 3. Navier-Stokes equation: Top:Re = 100时圆柱绕流的不可压缩流动和动态旋涡脱落。时空训练数据对应于圆柱尾流中描绘的矩形区域。Bottom:流向和横向速度分量\(u( t , x , y)\)和\(v( t , x , t)\)的训练数据点位置。
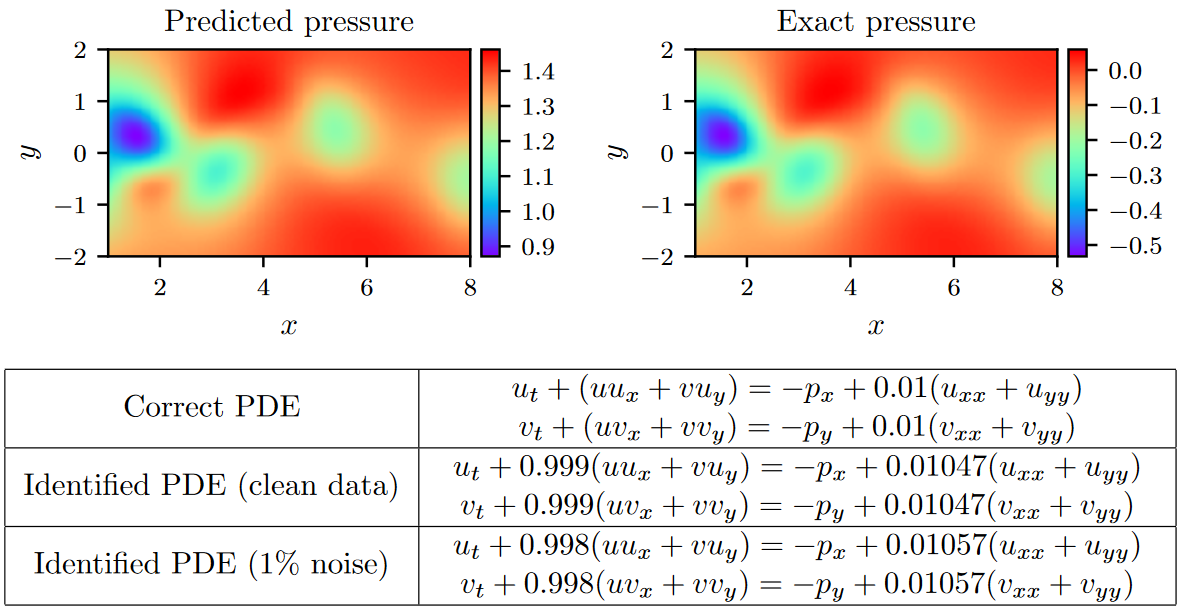
Figure 4. Navier-Stokes equation: Top:预测和精确的瞬时压力场p( t , x , y)在一个代表时刻。根据定义,压力可以恢复到一个常数,因此可以证明两个地块之间的大小不同。这种显著的定性一致性突出了物理信息的神经网络识别整个压力场的能力,尽管在模型训练过程中没有使用关于压力的数据。Bottom:通过学习λ 1,λ 2和p( t , x , y)得到的辨识偏微分方程和修正偏微分方程。
到目前为止,我们的方法假设分散的数据在整个时空域都是可用的。然而,在许多实际感兴趣的情况下,人们可能只能在不同的时间点观察系统。在接下来的章节中,我们介绍了一种不同的方法,该方法仅使用两个数据快照来处理数据驱动的发现问题。我们将看到,通过使用经典的Runge - Kutta时间步进方案,人们可以构建离散时间物理信息神经网络,即使在数据快照之间的时间间隔非常大的情况下,也可以保持较高的预测精度。
4.2. 离散时间模型
我们首先将q级Runge - Kutta方法[ 45 ]的一般形式应用于方程( 1 )并得到: \[ \begin{aligned}&u^{n+c_i}=u^n-\Delta t\sum_{j=1}^qa_{ij}\mathcal{N}[u^{n+c_j};\lambda],&i=1,\ldots,q,\\&u^{n+1}=u^n-\Delta t\sum_{j=1}^qb_j\mathcal{N}[u^{n+c_j};\lambda].\end{aligned} \tag{20} \] 式中,\(u^{n+c_j}(x) = u(t^n+c_j\Delta t,x),j=1,\cdots,1\)为系统在\(t^n+c_j\)时刻的隐藏状态。这种通用形式同时包含隐式和显式时间步进格式,取决于参数\({ a_{ij},b_j,c_j }\)的选择。式(20)可等价表示为: \[ \begin{aligned}&u^n=u_i^n,\quad i=1,\ldots,q,\\&u^{n+1}=u_i^{n+1},\quad i=1,\ldots,q.\end{aligned} \tag{21} \] 其中 \[ \begin{aligned}&u_i^n:=u^{n+c_i}+\Delta t\sum_{j=1}^qa_{ij}\mathcal{N}[u^{n+c_j};\lambda],\quad i=1,\ldots,q,\\&u_i^{n+1}:=u^{n+c_i}+\Delta t\sum_{j=1}^q(a_{ij}-b_j)\mathcal{N}[u^{n+c_j};\lambda],\quad i=1,\ldots,q.\end{aligned} \tag{22} \] 我们通过放置一个多输出神经网络先验来进行 \[ \begin{bmatrix}u^{n+c_1}(x),\ldots,u^{n+c_q}(x)\end{bmatrix}. \tag{23} \] 这个先验假设和方程( 22 )一起产生了两个物理信息的神经网络 \[ \begin{bmatrix}u_1^n(x),\ldots,u_q^n(x),u_{q+1}^n(x)\end{bmatrix}, \tag{24} \]
\[ \begin{bmatrix}u_1^{n+1}(x),\ldots,u_q^{n+1}(x),u_{q+1}^{n+1}(x)\end{bmatrix}. \tag{25} \]
分别给定系统在tn和tn + 1时刻的两个不同时间快照\(\{x_n,u_n\}\)和\(\{x_{n+1},u_{n+1}\}\)上的噪声测量,通过最小化误差平方和,可以训练神经网络( 23 )、( 24 )和( 25 )的共享参数以及微分算子的参数λ: \[ SSE=SSE_n+SSE_{n+1}, \tag{26} \] 其中 \[ \begin{aligned}SSE_n&:=\sum_{j=1}^q\sum_{i=1}^{N_n}|u_j^n(x^{n,i})-u^{n,i}|^2,\\\\SSE_{n+1}&:=\sum_{j=1}^q\sum_{i=1}^{N_{n+1}}|u_j^{n+1}(x^{n+1,i})-u^{n+1,i}|^2.\end{aligned} \] 式中,\(x^n=\{x^{n,i}\}_{i=1}^{N_n},u^n=\{u^{n,i}\}_{i=1}^{N_n},x^{n+1}=\{x^{n+1,i}\}_{i=1}^{N_{n+1}},u^{n+1}=\{u^{n+1,i}\}_{i=1}^{N_{n+1}}\)。
4.2.1. Example (Kortewegde Vries Equation)
我们最后的例子旨在突出所提出的框架处理涉及高阶导数的控制偏微分方程的能力。在这里,我们考虑浅水表面上波的数学模型;Korteweg-de Vries (KdV)方程。该方程也可以看作是添加了dispersive项的Burgers方程。KdV方程与物理问题有着千丝万缕的联系。它描述了长一维波在许多物理环境中的演化。这些物理环境包括具有弱非线性恢复力的浅水波、密度分层海洋中的长内波、等离子体中的离子声波、晶格上的声波等。此外,KdV方程是连续极限下Fermi-Pasta-Ulam问题中string的控制方程[ 48 ]。KdV方程为: \[ u_t+\lambda_1uu_x+\lambda_2u_{xxx}=0, \tag{27} \] 其中\((\lambda_1,\lambda_2)\)为未知参数。对于KdV方程,方程( 22 )中的非线性算子由下式给出: \[ \mathcal{N}[u^{n+c_j}]=\lambda_1u^{n+c_j}u_x^{n+c_j}-\lambda_2u_{xxx}^{n+c_j} \] 通过最小化误差平方和( 26 ),可以学习神经网络( 23 )、( 24 )和( 25 )的共享参数以及KdV方程的参数\(λ = ( λ1 , λ2)\)。
为了获得一组训练和测试数据,我们使用常规谱方法对式( 27 )进行模拟。具体来说,从初始条件\(u(0,x)=cos(πx)\)出发,假设周期性边界条件,利用Chebfun程序包[ 40 ]对式( 27 )积分至最终时刻t = 1.0,采用512阶谱Fourier离散和四阶显式Runge - Kutta时间积分器,时间步长\(∆t = 10 ^{- 6}\)。利用该数据集,我们提取了\(t^n = 0.2\)和\(t^{n + 1} = 0.8\)时刻的两个解的快照,并使用\(N_n = 199\)和\(N_{n + 1} = 201\)对其进行随机子采样,生成训练数据集。然后,我们利用这些数据通过使用L-BFGS[35]最小化方程( 26 )的误差平方和来训练一个离散时间的物理信息神经网络。这里使用的网络结构包括4个隐藏层,每层50个神经元和一个输出层,预测q Runge - Kutta stages的解,即\(u^{n+c_j}(x),j=1,\cdots,q\),其中q为经验选取,通过设定本算例的时间步长∆t = 0.6(这是由于隐式Runge - Kutta格式的理论误差估计表明其截断误差为\(\mathcal O(∆t^{2q})\)),得到机器精度阶次的时间误差累积。 \[ q=0.5\log\epsilon/\log(\Delta t), \tag{28} \] 本实验结果总结见图5。在顶层面板中,我们给出了精确解u( t , x),以及用于训练的两个数据快照的位置。在中间面板中给出了精确解和训练数据的更详细的概述。值得注意的是,方程( 27 )的复杂非线性动力学如何导致两个报告快照在解的形式上存在显著差异。尽管存在这些差异,并且两个训练快照之间存在较大的时间间隔,但无论训练数据是否被噪声污染,我们的方法都能够正确识别未知参数。具体来说,对于无噪声训练数据的情况,估计\(λ_1\)和\(λ_2\)的误差分别为0.023%和0.006%,而训练数据中含有1%噪声的情况分别为0.057%和0.017%。
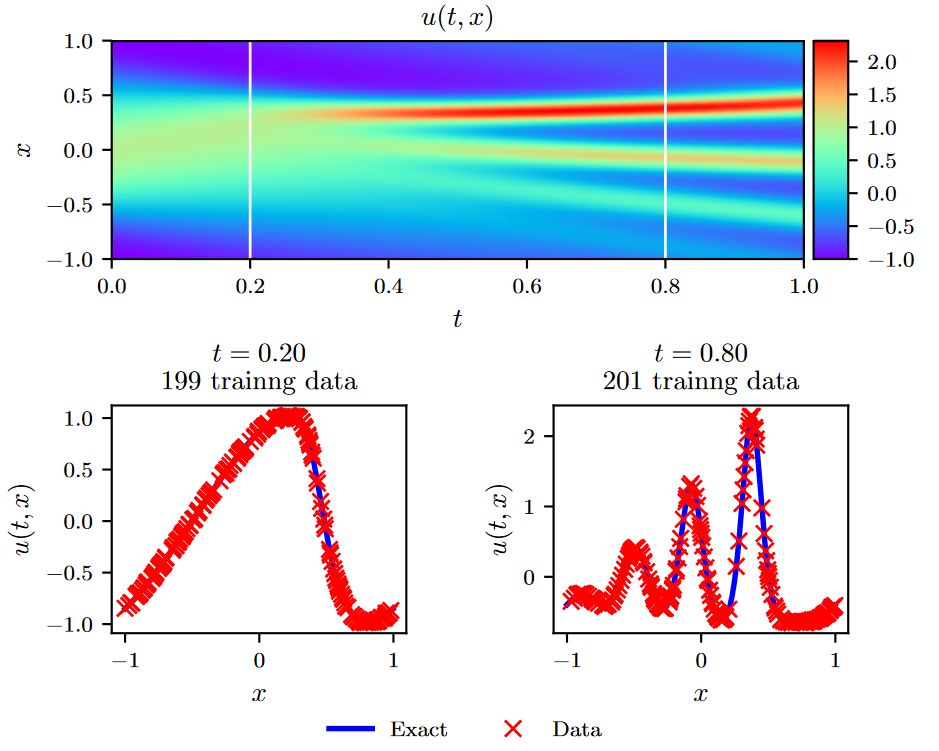

Figure 5: KdV equation: Top:解u( t , x)以及两个训练快照的时间位置。Middle:对应于顶部面板中虚线竖线所描绘的两个时间快照的训练数据和精确解。Bottom:结合学习λ 1,λ 2得到的辨识偏微分方程对偏微分方程进行修正。
5. 总结
我们引入了物理信息神经网络,这是一类新的通用函数逼近器,能够编码支配给定数据集的任何潜在物理规律,并且可以用偏微分方程来描述。在这项工作中,我们设计了数据驱动的算法来推断一般非线性偏微分方程的解,并构建计算高效的物理信息代理模型。由此产生的方法为计算科学中的各种问题展示了一系列有希望的结果,并为赋予深度学习强大的数学物理能力来建模我们周围的世界开辟了道路。由于深度学习技术在方法和算法方面的发展都在继续快速增长,我们认为这是一项及时的贡献,可以造福于广泛的科学领域的实践者。能够享受这些好处的具体应用包括但不限于数据驱动的物理过程预测、模型预测控制、多物理/多尺度建模与仿真。
然而,我们必须注意到,所提出的方法不应该被视为求解偏微分方程(例如,有限元、谱方法等.)的经典数值方法的替代。这些方法在过去的50年中已经成熟,并且在许多情况下满足实际中所要求的鲁棒性和计算效率标准。正如第3.2节所倡导的,我们的信息是,经典的方法如Runge - Kutta时间步进格式可以与深度神经网络和谐共存,并且在构造结构化预测算法时提供了宝贵的直觉。此外,后者的实现简单性极大地有利于新思想的快速开发和测试,为数据驱动的科学计算的新时代开辟了道路。
尽管提出了一系列有希望的结果,读者也许会同意这项工作创造了比它答案更多的问题。神经网络应该有多深/宽?到底需要多少数据?为什么该算法收敛到差分算子参数的唯一值,也就是说,为什么该算法不受差分算子参数局部最优的影响?对于更深的体系结构和更高阶的微分算子,网络是否遭受梯度消失的影响?可以通过使用不同的激活函数来缓解这种情况?是否可以在网络权值的初始化或数据的归一化方面进行改进?均方误差和误差平方和是合适的损失函数?为什么这些方法看起来对数据中的噪声非常鲁棒?我们如何量化与我们的预测相关的不确定性?在整个工作中,我们试图回答其中的一些问题,但我们观察到,对一个方程产生令人印象深刻的结果的特定设置可能会使另一个方程失败。诚然,需要更多的工作来共同建立这个领域的基础。
在更广泛的背景下,沿着寻找这些问题的答案的道路,我们认为这项工作倡导机器学习和经典计算物理之间的富有成效的协同作用,这有可能丰富这两个领域,并导致高影响力的发展。
